# 给这个 notebook 运行一些启动代码

import random
import numpy as np
from cs231n.data_utils import load_CIFAR10
import matplotlib.pyplot as plt

# 这是 notebook 的 magic 命令，可以让 matplotlib 的图表
# 显示在 notebook 中，而不是在一个新窗口里边
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

# 还是一些 magic 命令，让 notebook 重载外部的 python 模块；
# 见：http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2

# 加载原始 CIFAR-10 数据
cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'

# 清理变量，以防多次加载数据（这可能会导致内存问题）
try:
   del X_train, y_train
   del X_test, y_test
   print('Clear previously loaded data.')
except:
   pass

X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)

# 完整性测试，打印训练集和测试集的大小
print('Training data shape: ', X_train.shape)
print('Training labels shape: ', y_train.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)

# 可视化数据集中的一些用例
# 每种类型显示几张训练集中的图片
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
num_classes = len(classes)
samples_per_class = 7
for y, cls in enumerate(classes):
    idxs = np.flatnonzero(y_train == y)
    
    idxs = np.random.choice(idxs, samples_per_class, replace=False)

    for i, idx in enumerate(idxs):
        plt_idx = i * num_classes + y + 1
        plt.subplot(samples_per_class, num_classes, plt_idx)
        plt.imshow(X_train[idx].astype('uint8'))
        plt.axis('off')
        if i == 0:
            plt.title(cls)
plt.show()

# 作为练习，为了避免运行时间太长，这里再对数据进行采样，减小规模
num_training = 5000
mask = list(range(num_training))
X_train = X_train[mask]
y_train = y_train[mask]

num_test = 500
mask = list(range(num_test))
X_test = X_test[mask]
y_test = y_test[mask]

# 把图片数据变成一行 (32, 32, 3) -> 3072
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))

from cs231n.classifiers import KNearestNeighbor

# 创建 KNN 分类器实例
# 注意训练 KNN 分类器其实什么也没干，分类器只是简单地记录了一下数据
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)

# 打开 cs231n/classifiers/k_nearest_neighbor.py 并实现
# compute_distances_two_loops.

# 测试
dists = classifier.compute_distances_two_loops(X_test)
print(dists.shape)

# 我们可以将距离矩阵可视化：每行都表示一个测试用例和所有训练用例的距离
plt.imshow(dists, interpolation='none')
plt.show()

# 现在，实现方法 predict_labels，并运行下列代码：
# 令 k = 1（最近邻）
y_test_pred = classifier.predict_labels(dists, k=1)

# 计算并打印正确率
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))

y_test_pred = classifier.predict_labels(dists, k=5)
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))

# 接下来，我们使用部分向l量化，实现用单层循环来计算距离矩阵，
# 实现方法 compute_distances_one_loop，并运行如下代码：
dists_one = classifier.compute_distances_one_loop(X_test)

# 为了确认向量化结果的正确性，我们需要确保它的结果与简单方法一致。
# 判断两个矩阵相似的方法有很多，其中最简单的一种就是 F 范数。
# 两个矩阵的 F 范数是两个矩阵所有元素之差的平方和；
# 换句话说，就是把矩阵压成向量，然后计算他们的欧式距离。
difference = np.linalg.norm(dists - dists_one, ord='fro')
print('One loop difference was: %f' % (difference, ))
if difference < 0.001:
    print('Good! The distance matrices are the same')
else:
    print('Uh-oh! The distance matrices are different')

# 现在，在 compute_distance_no_loops 方法中实现全向量化版本的代码
# 并运行下列代码
dists_two = classifier.compute_distances_no_loops(X_test)

# 同样，通过计算两个矩阵的距离来验证结果
difference = np.linalg.norm(dists - dists_two, ord='fro')
print('No loop difference was: %f' % (difference, ))
if difference < 0.001:
    print('Good! The distance matrices are the same')
else:
    print('Uh-oh! The distance matrices are different')

# 比较一下不同实现的效率怎么样
def time_function(f, *args):
    """
    Call a function f with args and return the time (in seconds) that it took to execute.
    """
    import time
    tic = time.time()
    f(*args)
    toc = time.time()
    return toc - tic

two_loop_time = time_function(classifier.compute_distances_two_loops, X_test)
print('Two loop version took %f seconds' % two_loop_time)

one_loop_time = time_function(classifier.compute_distances_one_loop, X_test)
print('One loop version took %f seconds' % one_loop_time)

no_loop_time = time_function(classifier.compute_distances_no_loops, X_test)
print('No loop version took %f seconds' % no_loop_time)

# 你应该能看到使用全向量化方法之后性能明显提升了

# 注意：取决于你使用的机器
# 你可能会发现使用单层循序并没有性能的提升
# 相反还可能会更慢

num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]

X_train_folds = []
y_train_folds = []
################################################################################
# TODO:                                                                        #
# Split up the training data into folds. After splitting, X_train_folds and    #
# y_train_folds should each be lists of length num_folds, where                #
# y_train_folds[i] is the label vector for the points in X_train_folds[i].     #
# Hint: Look up the numpy array_split function.                                #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

X_train_folds = np.array_split(X_train, num_folds)
y_train_folds = np.array_split(y_train, num_folds)

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}


################################################################################
# TODO:                                                                        #
# Perform k-fold cross validation to find the best value of k. For each        #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times,   #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all     #
# values of k in the k_to_accuracies dictionary.                               #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
num_folds_count = np.ceil(X_train.shape[0]/num_folds)
for i in k_choices:
    list_acc = np.zeros(num_folds)
    for j in range(num_folds):
        start = int(j * num_folds_count)
        end = int((j+1) * num_folds_count)
        X_train_folds_train = np.delete(X_train,np.s_[start:end],0)
        y_train_folds_train = np.delete(y_train,np.s_[start:end],0)
        classifier.train(X_train_folds_train, y_train_folds_train)
        dists = classifier.compute_distances_no_loops(X_train_folds[j])
        y_test_pred = classifier.predict_labels(dists, k=i)
        num_correct = np.sum(y_test_pred == y_train_folds[j])
        accuracy = float(num_correct) / num_folds_count
        list_acc[j] = accuracy
    k_to_accuracies[i] = list_acc
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

# Print out the computed accuracies
for k in sorted(k_to_accuracies):
    for accuracy in k_to_accuracies[k]:
        print('k = %d, accuracy = %f' % (k, accuracy))

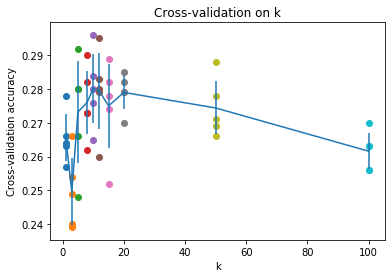
# plot the raw observations
for k in k_choices:
    accuracies = k_to_accuracies[k]
    plt.scatter([k] * len(accuracies), accuracies)

# plot the trend line with error bars that correspond to standard deviation
accuracies_mean = np.array([np.mean(v) for k,v in sorted(k_to_accuracies.items())])
accuracies_std = np.array([np.std(v) for k,v in sorted(k_to_accuracies.items())])
plt.errorbar(k_choices, accuracies_mean, yerr=accuracies_std)
plt.title('Cross-validation on k')
plt.xlabel('k')
plt.ylabel('Cross-validation accuracy')
plt.show()

# Based on the cross-validation results above, choose the best value for k,   
# retrain the classifier using all the training data, and test it on the test
# data. You should be able to get above 28% accuracy on the test data.
best_k = 10

classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
y_test_pred = classifier.predict(X_test, k=best_k)

# Compute and display the accuracy
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))