CCF 201512-4 送货
问题描述
为了增加公司收入,F公司新开设了物流业务。由于F公司在业界的良好口碑,物流业务一开通即受到了消费者的欢迎,物流业务马上遍及了城市的每条街道。然而,F公司现在只安排了小明一个人负责所有街道的服务。
任务虽然繁重,但是小明有足够的信心,他拿到了城市的地图,准备研究最好的方案。城市中有n个交叉路口,m条街道连接在这些交叉路口之间,每条街道的首尾都正好连接着一个交叉路口。除开街道的首尾端点,街道不会在其他位置与其他街道相交。每个交叉路口都至少连接着一条街道,有的交叉路口可能只连接着一条或两条街道。
小明希望设计一个方案,从编号为1的交叉路口出发,每次必须沿街道去往街道另一端的路口,再从新的路口出发去往下一个路口,直到所有的街道都经过了正好一次。
输入格式
输入的第一行包含两个整数n, m,表示交叉路口的数量和街道的数量,交叉路口从1到n标号。
接下来m行,每行两个整数a, b,表示和标号为a的交叉路口和标号为b的交叉路口之间有一条街道,街道是双向的,小明可以从任意一端走向另一端。两个路口之间最多有一条街道。
输出格式
如果小明可以经过每条街道正好一次,则输出一行包含m+1个整数p1, p2, p3, …, pm+1,表示小明经过的路口的顺序,相邻两个整数之间用一个空格分隔。如果有多种方案满足条件,则输出字典序最小的一种方案,即首先保证p1最小,p1最小的前提下再保证p2最小,依此类推。
如果不存在方案使得小明经过每条街道正好一次,则输出一个整数-1。
样例输入
4 5
1 2
1 3
1 4
2 4
3 4
样例输出
1 2 4 1 3 4
样例说明
城市的地图和小明的路径如下图所示。
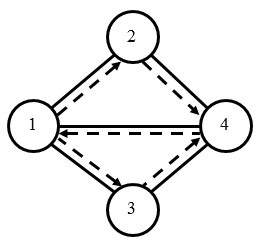
样例输入
4 6
1 2
1 3
1 4
2 4
3 4
2 3
样例输出
-1
样例说明
城市的地图如下图所示,不存在满足条件的路径。
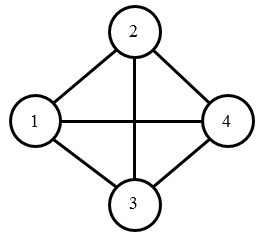
评测用例规模与约定
前30%的评测用例满足:1 ≤ n ≤ 10, n-1 ≤ m ≤ 20。
前50%的评测用例满足:1 ≤ n ≤ 100, n-1 ≤ m ≤ 10000。
所有评测用例满足:1 ≤ n ≤ 10000,n-1 ≤ m ≤ 100000。
解题说明
一笔画问题, 也就是求欧拉通路。根据欧拉定理, 对于这样一个无向连通图, 如果所有节点的度数都是偶数(情况1),那么这个图从任意点出发都一笔画; 如果有两个节点的度数是奇数(情况2), 其它节点度数为偶数, 那么从任一奇点出发能一笔画, 且终点为另一奇点。其余情况都不能一笔画。因此, 首先要判断图是不是连通的, 然后判断是不是这两种情况中的1个,不是得话直接输出-1返回。如果从1出发一定能一笔画的话, 除非遇到走不通的情况, 否则无论你怎么画都跳不出情况1和情况2。情况1画一条边,就会变成情况2, 情况2画一条边可能还是情况2,或者就是变成情况1。只有一种情况会发生改变, 那就是接下来要画的边的另一端度数是1的时候, 这样画下去会使得新的起点变成与图的其它部分分隔的单点, 就再也走不通了。这时候, 我们不能画这条边, 但根据欧拉定理,图明明又是能够一笔画的, 这就说明这条边只能最后画。 于是我们可以直接把这条边去掉, 把另一端的顶点压栈, 作为一笔画的最后一点。如此类推, 当出现这种情况时就把点压栈。最后,再弹出来, 就可以得到一个一笔画的顶点序列。而且, 我们发现这个过程其实就是dfs的过程。即dfs的逆后序列就是一个一笔画的序列。至于要字典序最小,只需要事先对邻接表按升序排序即可。
#include <iostream>
#include <vector>
#include <map>
#include <stack>
#include <algorithm>
using namespace std;
map<int,int> con;
vector<int> *mp;
stack<int> st;
bool marked[10001][10001];
int id[10001];
int N,M,COU;
// 带路径压缩的quick-union
int _find(int p) {
if(p==id[p]) {
return p;
}
return (id[p]=_find(id[p]));
}
bool _union(int p,int q) {
p=_find(p);
q=_find(q);
if(p==q) {
return false;
}
id[p]=q;
return true;
}
// 深度优先搜索
void dfs(int s) {
int len=mp[s].size();
for(int i=0; i<len; i++) {
int e=mp[s][i];
if(!marked[s][e]){
marked[s][e]=marked[e][s]=true;
dfs(e);
}
}
st.push(s);
}
int main(void) {
int s,e;
cin>>N>>M;
mp=new vector<int>[N+1];
for(int i=1; i<=N; i++) {
id[i]=i;
}
for(int i=0; i<M; i++) {
cin>>s>>e;
_union(s,e);
mp[s].push_back(e);
mp[e].push_back(s);
}
// union-find判断连通性
bool ok=true;
int fa=_find(1);
for(int i=2; i<=N; i++) {
if(_find(i)!=fa) {
ok=false;
break;
}
}
if(ok) { // 如果连通
// 升序排序
for(int i=1; i<=N; i++) {
sort(mp[i].begin(),mp[i].end());
}
COU=0;
for(int i=1; i<=N; i++) {
con[i]=mp[i].size();
if(con[i]%2) {
COU++;
}
}
// 符合欧拉通路条件,进行深搜,得到后序列
if(COU==0||COU==2&&con[1]%2) {
dfs(1);
int t;
// 逆后序列即为符合条件的通路
while(!st.empty()){
t=st.top();
cout<<t<<' ';
st.pop();
}
cout<<endl;
} else { // 不符合欧拉环路条件
cout<<-1<<endl;
}
} else { // 如果不连通
cout<<-1<<endl;
}
delete mp;
return 0;
}